يقدم لكم موقع اقرأ مجموعة من أمثلة على تحليل العبارة التربيعية ، و ورقة عمل تحليل العبارة التربيعية ، و مسائل على درس تحليل العبارة التربيعية ، و أمثلة على حل المعادلات التربيعية ، و حل أسئلة درس تحليل العبارة التربيعية للصف التاسع ، و تحليل العبارة التربيعية باكمال المربع ، لكل الطلاب الذين يبحثون عن جمل وأمثلة على تحليل العبارة التربيعية لتسهل عليهم فهم هذا الدرس تابعوا معنا:
أمثلة على تحليل العبارة التربيعية
لتحليل المعادلة (العبارة) التربيعة يتم إيجاد قيمة (س) التي لو تم تعويضها في المعادلة ستكون قيمة (ص) تساوي صفراً، بمعنى آخر: ما هي قيم الإحداثي السيني التي تجعل الإحداثي الصادي تساوي صفراً، وهي النقاط التي يقطع فيها المنحنى المحور السيني. وفيما يلي سوف نتعرف على أمثلة على تحليل العبارة التربيعية :
مثال ١ : جد حل المعادلة التربيعية س2 + 4 س = 16 بطريقة إكمال المربع.
- الحل: ترتيب المعادلة التربيعية لتكن على الصيغة العامة (س2 + 4 س – 16 = 0). إيجاد قيمة (ب / 2) 2 = (4 / 2)2 = 4 إضافة القيمة السابقة ومعكوسها للمعادلة التربيعية، س2 + 4 س + 4 – 4 – 16 = 0 بإعادة ترتيب المعادلة التربيعية: (س2 + 4 س + 4) + (-16-4) = 0 بإعادة ترتيب المعادلة: (س+2)2 – 20 = 0 ومنه؛ (س+2)2 = 20 بأخذ الجذر التربيعي للطرفين، ونقل العدد 2 للطرف الآخر ينتج؛ س= -6.47، س= 2.47.
مثال ٢ : جد حل المعادلة التربيعية س2 + 6 س -2 بطريقة إكمال المربع.
- الحل: كتابة المعادلة التربيعية لتكن على الصيغة العامة: س2 + 6 س -2= 0. إيجاد القيمة (ب / 2) 2 = (6 / 2)2 = 9. إضافة القيمة السابقة ومعكوسها للمعادلة التربيعية، س2 + 6 س + 9 – 9 -2= 0. بإعادة ترتيب المعادلة (س2 + 6 س + 9 ) -9 -2= 0. ومنه؛ س2 + 6 س + 9 = 11 وبتحليل المعادلة إلى عواملها؛ (س+3)2 = 11 بأخذ الجذر للطرفين، فتصبح س= (11 √)-3، أو س = -(11 √)-3
قد يهمك :
- امثلة على ثنائية القطب
- أمثلة على كان وأخواتها
- أمثلة على كان وأخواتها من القران
- أمثلة على كم الاستفهامية والخبرية
- أمثلة على اسم الفاعل
- امثلة على همزة الوصل والقطع من القرآن
- أمثلة على اسم المصدر
- أمثلة على جزم الفعل المضارع
- أمثلة على التاء المربوطة والتاء المفتوحة
ورقة عمل تحليل العبارة التربيعية
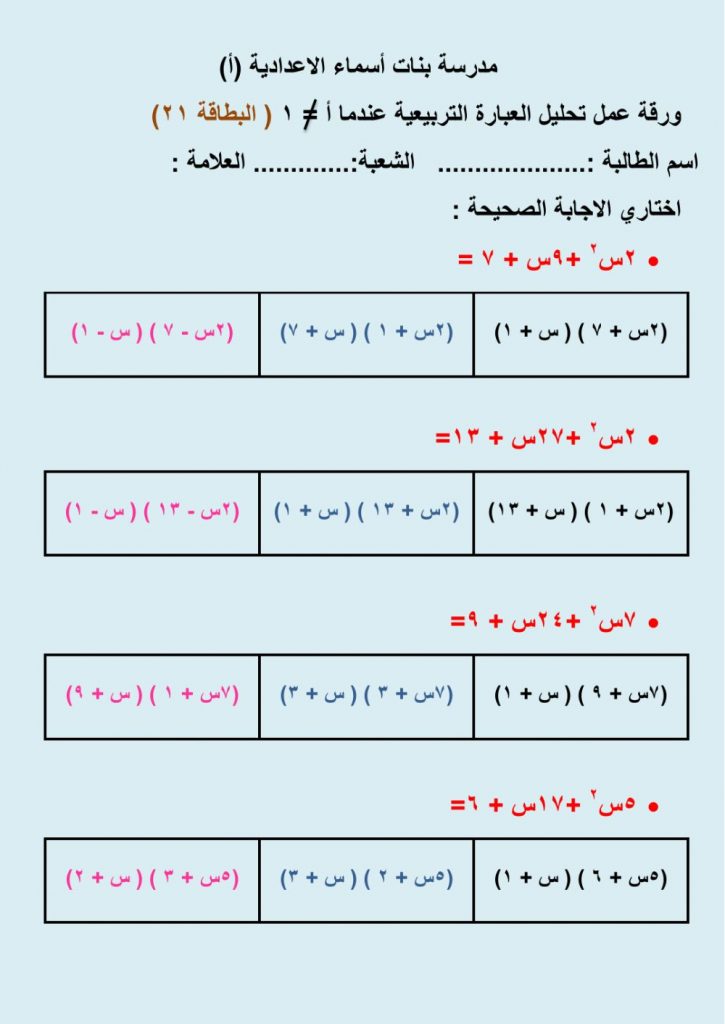
وفيما يلي سوف نتعرف على نموذج جاهز لورقة عمل تحليل العبارة التربيعية ، تعرفوا عليها الآن :
النموذج :
مسائل على درس تحليل العبارة التربيعية
عزيزي الطالب هل تبحث عن نماذج مسائل على درس تحليل العبارة التربيعية ، تساعدك في فهم هذا الدرس ، فريق منصة اقرأ يقدم لكم مجموعة من فيديوهات التعليمية التي يتم من خلالها شرح كيفية حل هذه المسائل ، تابعوا معنا :
فيديوهات تعليمية :
أمثلة على حل المعادلات التربيعية
وفيما يأتي نقدم لكم من خلال هذه الفقرة من على منصتنا اقرأ بعض الأمثلة على على حل المعادلات التربيعية :
مثال ١ : ما ناتج تحليل العبارة التربيعية الآتية س2 + 5س = 0؟
- الحل: يتم حل المثال الآتي باستخدام الخطوات الآتية: إيجاد عامل مشترك من كلا الحدين، وهو هنا “س”. تصبح المسألة س (س + 5). وبالتالي فإن ناتج التحليل هو س (س+5).
مثال ٢ : ما حل العبارة التربيعية الآتية س2 + 16 = 10س؟
الحل: يمكن تحليل العبارة التربيعية الآتية بالخطوات الآتية: كتابة المعادلة بالشكل الصحيح بحيث يكون الطرف الآخر يساوي صفراً، وذلك كما يأتي س2 -10س + 16= 0. إيجاد العوامل باستخدام طريقة إيجاد العوامل، للحصول على العوامل (س – 2)(س – 8). إيجاد قيمة العوامل عن طريق المساواة بالصفر، وذلك كما يأتي: س – 2=0، س-8=0. وبالتالي فإن قيمة العوامل هي س=2، س=8.
حل أسئلة درس تحليل العبارة التربيعية للصف التاسع
و لكل طلاب صف التاسع نقدم لكم من خلال السطور التالية حل أسئلة درس تحليل العبارة التربيعية للصف التاسع ، كل ما عليكم هو تحميل الرابط أسفله :
- حل أسئلة درس تحليل العبارة التربيعية للصف التاسع : من هنا .
تحليل العبارة التربيعية باكمال المربع
تحليل العبارة التربيعية باكمال المربع ، يُمكن تعريف المعادلة التربيعية (Quadratic Equation) بأنّها المعادلة التي تظهر بالصيغة العامّة الآتية:[١] أس² + ب س + ج = 0
خطوات حل المعادلة التربيعية بطريقة اكمال المربع :
1-أوجد نصف ب (معامل س)
2-ربع الناتج في الخطوة (1)
3-اضف الناتج من الخطوة (2) الى س^2+ب س
مثال(1) : اوجد قيمة ج التي تجعل ثلاثية الحدود مربعا كاملا. س^2-8س+ج
- نتبع الخطوات السابقة (نصف 8=4)
- مربع العدد 4 هو 16
- اذا الحل هو س^2-8رس+16
مثال (2) : حل المعادلة التالية بطريقة إكمال المربع س^-6س+12=19
- س^2-6س=7 (اطرح 12 من الطرفين )
- س^2-6س+9=7+9 (اضف مربع نصف معامل س للطرفين )
- (س-3)^2 =16 (حلل الطرف الايمن واحسب الطرف الايسر)
- (س-3)=+ او – 4 (الجذر للطرفين)
- س= (+ او – 4 + 3 ( اضف +3 للطرفين)
- س=4+3 او س=-4+3 (افصل الحلين)
- س=7 او س=-1 (حلان للمعادلة )
- الحل= (7,-1) (اكتب مجموعة الحل)